La curva de Philips
La curva de Phillips es una relación macroeconómica inversa entre el desempleo y la inflación de un estado. En resumen, establece, supuestamente, que en un eje de coordenadas se ubica en las abscisas a la tasa de desempleo y en las ordenadas a la tasa de inflación, se logrará obtener una curva en pendiente negativa similar a la de la demanda.
Esto es por supuesto una simple casualidad y no debe tomarse como un factor técnico a tenerse en cuenta. No obstante, este fenómeno representa una de las casualidades más entretenidas de la economía.
Un fenómeno visual
De manera curiosa, en ciertos periodos económicos de bonanza la curva de Phillips de Japón toma una forma extremadamente parecida a la del país, algo que podemos considerar como una pareidolia. En ella pueden diferenciarse las islas de Shikoku, la más pequeña de las cuatro islas que forma al Japón, Honshu, la isla «principal», así como Hokkaido y Kyushu, las islas del norte y sur respectivamente.
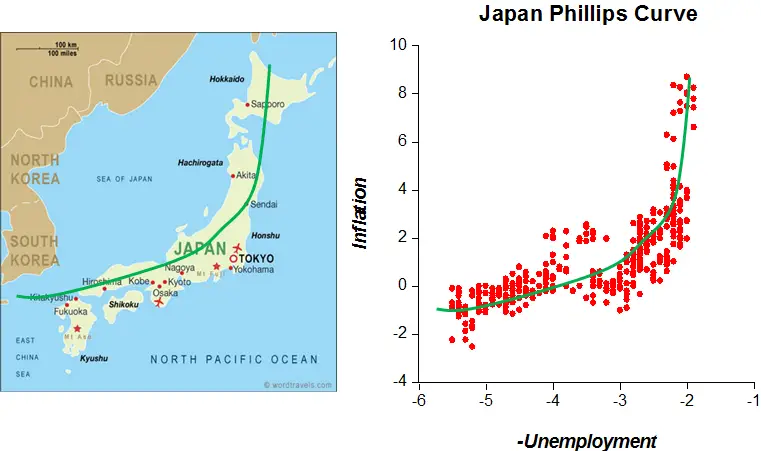
Como vemos en la imagen anterior la similitud es muy notable.
Si bien hoy está relación ha caído en desuso, ya que su precisión desaparece a medida que la relación se mantiene a largo plazo, el fenómeno de la curva pareciéndose a su país de origen no sólo ha ocurrido con Japón, sino además pudo observarse en Indonesia, Italia, Canadá, Alemania, Chile y muchos otros países.
Este fenómeno llevó al economista Peter Goodman a realizar un ensayo sobre la relación entre la forma geográfica del país y la curva de Phillips. Según Goodman, a medida que la relación se mantiene a largo plazo, la curva tiene a verticalizar su trayectoria, por lo que, dadas ciertas variables, pueda llegar a semejar, a manera de pareidolia, la forma de ciertos tipos de países.
Una economía muy estable: la economía japonesa es tan estable a largo paso que el país asiático posee las empresas más antiguas del mundo: Las empresas más viejas del mundo, las empresas milenarias de la tierra.
Un tanto similar a esto es el proyecto que intentaba buscar la forma de países, bosques y objetos dentro del conjunto de Mandelbrot utilizando datos estadísticos de dichos objetos en las variables de las formulas fractales.
Curiosamente este tipo de fenómenos macroeconómicos visuales son más comunes de lo esperado. Como mencionamos anteriormente esto no significa nada en especial, es simplemente una coincidencia visual similar a las pareidolias. No obstante, eso no hace que las mismas dejen de ser extremadamente curiosas.
Como mencionábamos anteriormente hay investigadores que buscan similitudes a distintos puntos geográficos en los fractales, más especialmente el conjunto de Mandelbrot. Curiosamente, la naturaleza le lleva la humanidad mucha ventaja al respecto, ya que muchos patrones evolutivos utilizan patrones fractales para maximizar su eficiencia: Fractales en la naturaleza, cómo la evolución ha creado fractales naturales.

Más sobre fenómenos económicos
― La burbuja inmobiliaria que destruyó a la empresa más antigua del mundo