Flatland, la obra que explica las dimensiones del universo
Flatland es una obra cuyo objetivo fue el de explicar de manera clara como es vivir en un universo 2D y que pasa si se introduce otra dimensión.
Etiqueta Matemática
Crisipo de Solos, el filósofo griego del cual todo se ha perdido
Hace más de 2200 un influyente filósofo y matemático, Crisipo de Solos, refundó el pensamiento estoico. El destino quiso que todos sus textos de pierdan.
El experimento para validar la democracia de Francis Galton
Con el fin de demostrar la importancia de la democracia, el matemático Francis Galton desarrolló un experimento para demostrar la sabiduría de las masas.
El asombroso fractal Buddhabrot, la imagen fractal que se asemeja a Buda
El Buddahbrot o Budabrot es un tipo de fractal desprendido del conjunto Mandelbrot famoso por su similitud visual con las estatuas budistas de Buda.
Olas dentro de una burbuja de agua en la Estación Espacial Internacional
El astronauta de la NASA Don Pettit durante la Expedition 6 a la Estación Espacial realizó varios experimentos con burbujas y olas en micro gravedad.
Visualización de datos en Wikipedia y Amazon
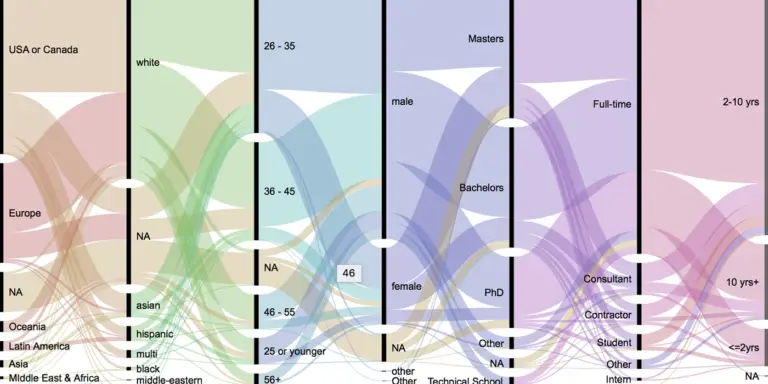
Mediante avanzadas técnicas de visualización de datos se ha logrado visualizar las estructuras de los datos en Wikipedia, Amazon y otras bases de datos.
El texto perdido de Arquímedes, el palimpsesto de Arquímedes
El texto perdido de Arquímedes pasó siglos oculto debajo de un iluminismo medieval cuando un monje necesitado de papel pinto encima de este.
Fractales en la naturaleza, cómo la evolución ha creado fractales naturales
La eficiencia evolutiva ha llevado a que a lo largo de los millones de años de evolución varios vegetales adquieren formaciones fractales en su estructura.
Japón y la Curva de Phillips, una llamativa coincidencia macroeconómica
Durante ciertos periodos económicos de bonanza la curva de Phillips de Japón toma a su vez una forma extremadamente parecida a la silueta del país.
El papiro egipcio de Rhind, el texto matemático más antiguo de la historia
La influencia egipcia en los inicios de la ciencia ha sido monumental. El primer texto matemático en la Historia: el papiro de Rhind.