Flatland, la obra que explica las dimensiones del universo
Flatland es una obra cuyo objetivo fue el de explicar de manera clara como es vivir en un universo 2D y que pasa si se introduce otra dimensión.
Etiqueta Dimensiones
La perspectiva de Jastrow, cuando dos tamaños iguales parecen distintos
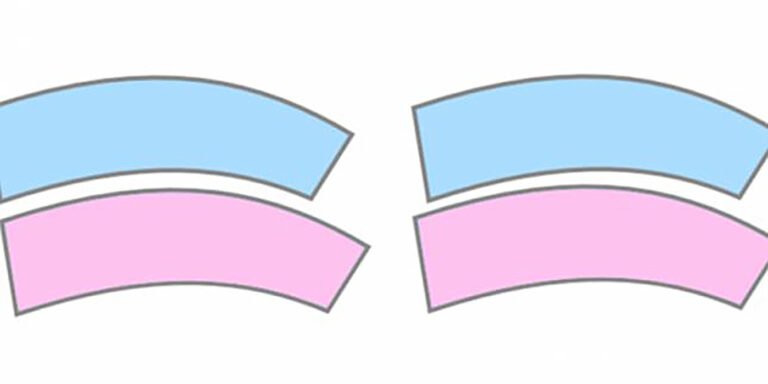
La perspectiva de Jastrow es un fenómeno visual de alteración de la percepción en el cual dos objetos del mismo tamaño parecen tener distintos tamaños.
Halucii, una animación basada en el arte matemático de Escher
Halucii es una genial animación que utiliza los conceptos y el estilo desarrollado a principios del siglo XX por Maurits Escher.
El arte matemático de Escher, las mejores ilustraciones de su obra
A principios del siglo XX un arquitecto holandés revolucionó el arte combinando la ilustración con las matemáticas. El arte de Escher.